本文共 5176 字,大约阅读时间需要 17 分钟。
文章目录
Tomcat介绍
- 免费的、开放源代码的Web应用服务器,属于轻量级应用服务器 在中小型系统和并发访问用户不是很多的场合下被普遍使用 是开发和调试JSP程序的首选
- Apache软件基金会(Apache Software Foundation)Jakarta项目中的一个核心项目 由Apache、Sun和一些公司及个人共同开发而成 深受Java爱好者的喜爱,并得到部分软件开发商的认可 目前比较流行的Web应用服务器
Tomcat组件
-
Tomcat由一系列的组件构成,其中核心的组件有三个:
Web容器------完成Web服务器的功能。
Servlet 容器------名字为catalina, 用于处理Servlet代码。 JSP容器------用于将JSP动态网页翻译成Servlet代码。
JavaServlet
JavaServlet是运行在Web服务器或应用服务器上的程序,它是作为来自web浏览器或其他HTTP客户端的请求和HTTP服务器上的数据库或应用程序之间的中间层。使用Servlet,可以收集来自网页表单的用户输入,呈现来自数据库或者其他源的记录,还可以动态创建网页。与CGI (公共网关接口)功能相类似。
JSP容器
JSP全称:Java Server Pages
是一种动态网页开发技术。它使用JSP标签在HTML网页中插入Java代码。标签通常以<%开头 以%>结束。JSP是一 种Java servlet,主要用于实现Java web应用程序的用户界面部分。 JSP 通过网页表单获取用户输入数据、访问数据库及其他数据源,然后动态地创建网页。Tomcat部署步骤
在部署 Tomcat 之前必须安装好 jdk,因为 jdk 是 Tomcat 运行的必要环境。
关闭防火墙,将安装 Tomcat 所需软件包上传到 /opt 目录下
systemctl stop firewalld.servicesystemctl disable firewalld.servicesetenforce 0
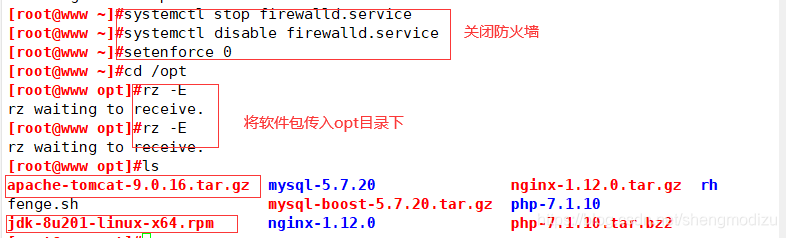
安装JDK
#查询指定软件包的文件列表rpm -qpl jdk-8u201-linux-x64.rpm#安装rpm -ivh jdk-8u201-linux-x64.rpmjava -version
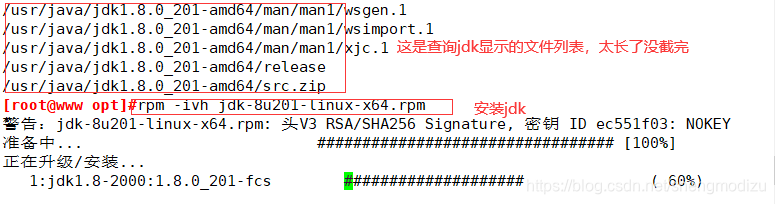

设置 JDK 环境变量
#profile.d相当于profile的扩展地盘vim /etc/profile.d/java.shexport JAVA_HOME=/usr/java/jdk1.8.0_201-amd64export CLASSPATH=.:$JAVA_HOME/lib/tools.jar:$JAVA_HOME/lib/dt.jarexport PATH=$JAVA_HOME/bin:$PATHsource /etc/profile.d/java.shjava -version-------java.sh中补充的知识点-----------------------------------CLASSPATH:编译、运行Java程序时,JRE 会去该变量指定的路径中搜索所需的类( .class)文件。dt.jar:是关于运行环境的类库,主要是swing 的包。tools.jar:主要是一 些 jdk 工具的类库,包括 javac, java,javap, javadoc等。JDK:java development kit ( java开发工具)JRE:java runtime environment ( java运行时环境)JVM:java virtuak machine (java虚拟机) ,使 java程序可以在多种平台上运行class文件。


编写一个java脚本来验证是否安装成功
vim dizu.java#编写一个java程序,输出“hello world!”public class dizu { public static void main(String[] args){ System.out.println("Hello World!"); }}#检测JDK环境是否设置成功javac dizu.javajava dizu 

安装启动 Tomcat
cd /opt/tar zxvf apache-tomcat-9.0.16.tar.gzmv apache-tomcat-9.0.16 /usr/local/tomcat##启动tomcat##/usr/local/tomcat/bin/startup.shnetstat -natp | grep 8080#使用浏览器访问Tomcat的主页 http://192.168.249.10:8080

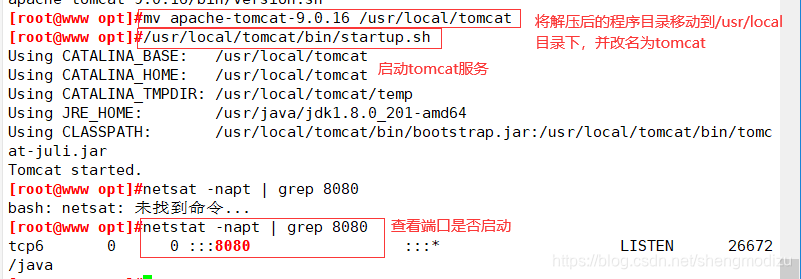
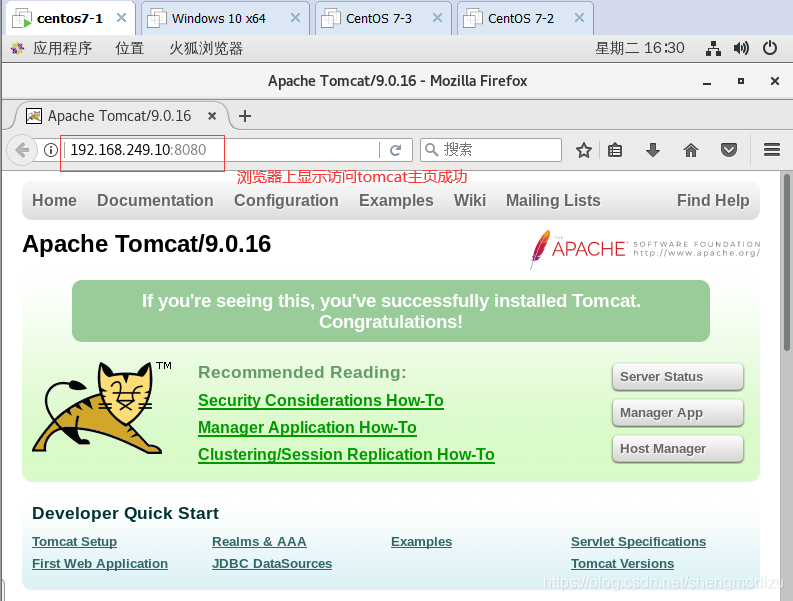
优化 Tomcat 启动速度
第一次启动 tomcat 可能会发现 tomcat 启动很慢,默认情况下可能需要几十秒,此时可以修改 jdk 参数进行优化。
vim /usr/java/jdk1.8.0_201-amd64/jre/lib/security/java.security#修改117行;##/dev/random和/dev/urandom都是伪终端,但是/dev/urandom提供的数据流更快securerandom.source=file:/dev/urandom#创建一个软连接,将tomcat的命令放入/usr/local/binln -s /usr/local/tomcat/bin/* /usr/local/bin/#重启Tomcatshutdown.shstartup.sh

Tomcat主要目录
查看目录命令:ll /usr/local/tomcat| 主要目录 | 用途 |
|---|---|
| bin | 存放启动和关闭Tomcat 的脚本文件,比较常用的是catalina. sh、startup.sh、 shutdown.sh 三个文件 |
| conf | 存放Tomcat 服务器的各种配置文件,比较常用的是server. xml、context . xml、tomcat-users.xml、 web. xml 四个文件. |
| lib | 存放Tomcat服务器的 jar 包,一 般不作任何改动,除非连接第三方服务,比如redis, 那就需要添加相对应的jar包 |
| logs | 存放Tomcat 日志 |
| temp | 存放Tomcat 运行时产生的文件 |
| webapps | 存放项目资源的目录 |
| work | Tomcat 工作目录,一般清除 Tomcat 缓存的时候会使用到 |
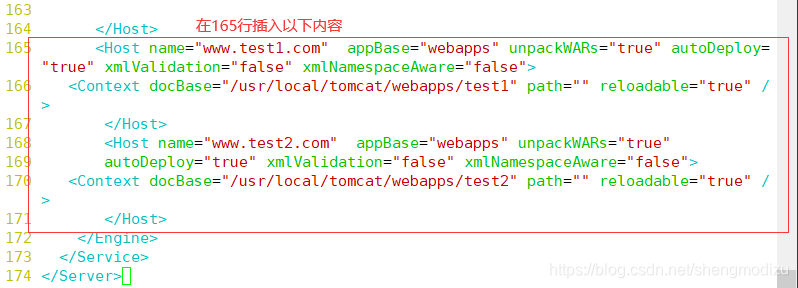
Tomcat 虚拟主机配置
很多时候公司会有多个项目需要运行,那么肯定不可能是一台服务器上运行多个Tomcat服务,这样会消耗太多的系统资源。此时,就需要使用到Tomcat虚拟主机。例如现在新增两个域名www.test1.com和www.test2.com,希望通过这两个域名访问到不同的项目内容。
创建test1和test2项目目录和文件
mkdir /usr/local/tomcat/webapps/test1mkdir /usr/local/tomcat/webapps/test2echo 'this is test1 page!' > /usr/local/tomcat/webapps/test1/index.jspecho 'this is test2 page!' > /usr/local/tomcat/webapps/test2/index.jsp

修改 Tomcat 主配置文件
vim /usr/local/tomcat/conf/server.xml #165行#重启服务;命令路径优化后可以直接使用shutdown.sh和startup.sh/usr/local/tomcat/bin/shutdown.sh/usr/local/tomcat/bin/startup.sh#----------------参数解释-----------------------------Host name :主机名appBase : Tomcat程序工作目录,相对路径为webapps,绝对路径为/usr/local/tomcat/webappsunpackWARs :是否解压war包autoDeploy :指示Tomcat运行时,如有新的WEB应用是否允许自动部署xmlValidation :是否验证xml文件执行有效性检验的标志xmlNamespaceAware :是否启用xml命名空间,设置该值与xmlValidation为true,表示对web.xml文件执行有效性检验docBase : WEB应用的目录path:设置访问的URI为WEB应用的根目录reloadable :是否在程序有改动时重新载入
浏览器访问验证
echo "192.168.249.10 www.test1.com www.test2.com" >> /etc/hosts

浏览器访问 http://www.test1.com:8080 页面显示 this is test1 page!
浏览器访问 http://www.test2.com:8080 页面显示 this is test2 page!
Tomcat 优化
Tomcat 默认安装下的缺省配置并不适合生产环境,它可能会频繁出现假死现象需要重启,只有通过不断压测优化才能让它最高效率稳定的运行。优化主要包括三方面,分别为操作系统优化(内核参数优化),Tomcat配置文件参数优化,Java虚拟机(JVM)调优。今天我们就了解一下Tomcat配置文件参数优化。
Tomcat配置文件参数优化
| 参数 | 作用 |
|---|---|
| maxThreads | Tomcat 使用线程来处理接收的每个请求,这个值表示Tomcat 可创建的最大的线程数,默认值是200。 |
| minSpareThreads | 最小空闲线程数,Tomcat 启动时的初始化的线程数,表示即使没有人使用也开这么多空线程等待,默认值是10。 |
| maxSpareThreads | 最大备用线程数,一旦创建的线程超过这个值,Tomcat 就会关闭不再需要的socket 线程。默认值是-1 ( 无限制)。一般不需要指定。 |
| URIEncoding | 指定 Tomcat 容器的 URL 编码格式,语言编码格式这块倒不如其它 Web 服务器软件配置方便,需要分别指定。 |
| connnectionTimeout | 网络连接超时,单位:亳秒,设置为 0 表示永不超时,这样设置有隐患的。通常默认20000亳秒就可以。 |
| enableLookups | 是否反查域名,以返回远程主机的主机名,取值为: true 或 false, 如果设置为false, 则直接返回IP 地址,为了提高处理能力,应设置为false。 |
| disableUploadTimeout | 上传时是否使用超时机制。应设置为true。 |
| connectionUploadTimeout | 上传超时时间,毕竟文件上传可能需要消耗更多的时间,这个根据你自己的业务需要自己调,以使 Servlet 有较长的时间来完成它的执行,需要与上一个参数一起配合使用才会生效。 |
| acceptCount | 指定当所有可以使用的处理请求的线程数都被使用时,可传入连接请求的最大队列长度,超过这个数的请求将不予处理,默认为100 个。 |
| compression | 是否对响应的数据进行GZIP压缩,off:表示禁止压缩; on:表示允许压缩 (文本将被压缩)、force:表示所有情况下都进行压缩,默认值为off,压缩数据后可以有效的减少页面的大小,一般可以减小1/3左右,节省带宽。 |
| compressionMinSize | 表示压缩响应的最小值,只有当响应报文大小大于这个值的时候才会对报文进行压缩,如果开启了压缩功能,默认值就是2048。 |
| compressableMimeType | 压缩类型,指定对哪些类型的文件进行数据压缩。 |
| noCompressionUserAgents=“gozilla, traviata” | 对于以下的浏览器,不启用压缩 |
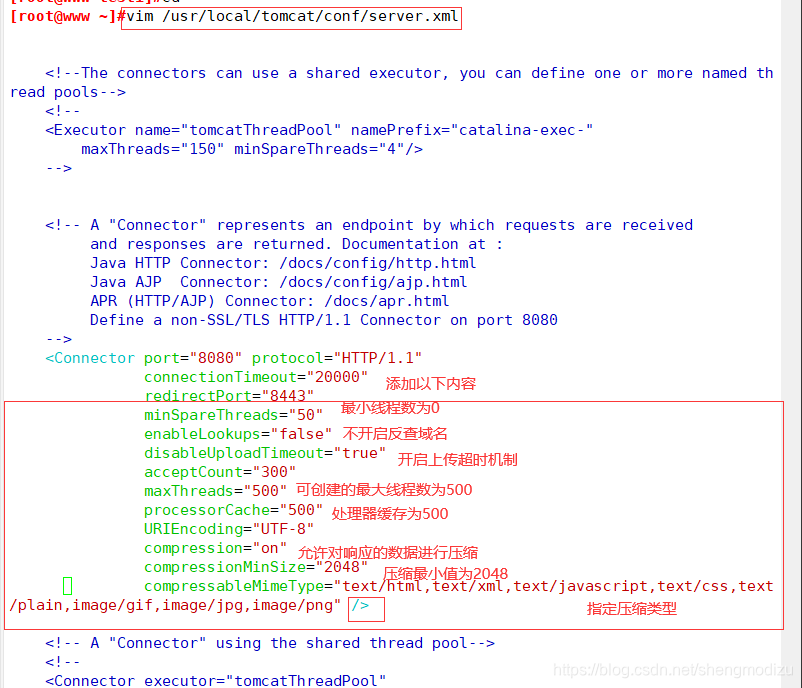
修改配置文件
vim /usr/local/tomcat/conf/server.xml#优化就直接用shutdown.sh和startup.sh/usr/local/tomcat/bin/shutdown.sh/usr/local/tomcat/bin/startup.sh

转载地址:http://pvis.baihongyu.com/